引自Fabian Suchanek的讲义。

 

总结：马尔科夫你需要知道这么几个点：

第一个是要知道如何形成马尔科夫随机场的条件，就是当有多个随机变量满足：Xi只由他的邻居决定，至于邻居是可以形成无向图，邻居是点，邻居和邻居的连线是边。

第二个要清楚的是Hammersley-Clifford-Theorem形成的条件，很容易，是说马尔科夫随机场里面的P都大于0的时候，这个也叫作矢量化，在CRF里面有提到，也就是当P大于0的时候，x也就是一条一条的rules，当他们成立的时候的概率等于势函数的乘积。

第三个要知道MRF和rules有什么关系，为什么要在这里运用MRF，MRF是可以计算所有KB的权重不同的时候的概率，概率是怎么算的呢，在第二条我讲过了，就是当rules成立的时候势函数的乘积，但是在计算KB的总权重时，并不是每个rules都会成立，我们根据式子，可以知道P是是函数的乘积，势函数是e的权重次方，e是单调递增函数，所以权重越大，那么势函数越大，那么P就越大，当权重最大的时候，也就是rules都成立的时候，就是KB权重最大的时候。

 

 

下图是一个表格，w代表possible world，X代表rules，例如hasSpouse之类的，F/T是随机身体成的答案，F代表对应的X不成立反之为T，P代表着出现该possible world的概率。

 

 

马尔科夫随机场MRF：由一系列随机变量组成，且它们满足：

 

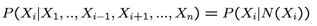
N(Xi) 表示Xi的邻居，也就是能决定Xi的东西

整个式子表示Xi只被它的邻居决定

 

下图为一个马尔科夫随机场

 

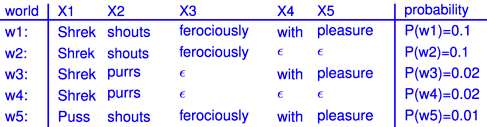
从图中我们可以看出X123是互相依赖的

X45是互相依赖的，因为4出现5也出现，4不出现5也不出现，这个道理对5也成立。

 

邻居Neighbors：互相依赖的就可以成为邻居，邻居之间可以形成无向图，也就是整个表格的cliques

表示邻居：N(X1) = {X2,X3} etc…

表示cliques：C1 = {X1,X2,X3}, C2 = {X1,X2,X3}

最大的clique：cliques中边最多的，此处是C1

 

Hammersley-Clifford-Theorem：若MRF中每个P都大于0，那么

 

 

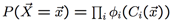
势函数：根据表格中的rules是否成立来计算

例如：

 

若条件成立得到的的是权重，那么势函数的结果是e的权重次方

 

我们有这些带权重的rules，我们想计算KB的各种possibleword出现的概率分布：可以使用MRF

 

我们设is(Ron, Immature)为X1，likes(H,Ron)为X2, type(H,sor)为X3，我们可得：

 

 

第一个式子是指若x1成立，那么得到权重10，若不成立则得到权重0，所以对应的势函数结果就是e的10次方或者是e的0次方。

最终P就是这三种情况的乘积。

 

MRF与MAXSAT：当W最大时得到的P就是KB权重最大的概率

P是势函数的成绩，势函数是e的权重次方，e是单调递增函数，所以权重越大那么势函数越大，那么P越大，所以要使P变大，最根本上是要让w变大，即使用梯度上升的方法使W变大。

公式推理：

使下面的式子最大：

 

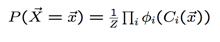
即：找到使此式子值最大的x

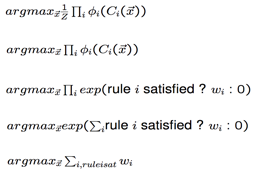
所以得到P至于W有关，所以尽量让w大一些。

 

正则化Normalization：因为要让P在0和1之间，所以把势函数的乘积除以了Z

 

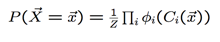
马尔科夫逻辑网Markov Logic Network：一些带权重的rules形成马尔科夫逻辑网，factor是势函数，当rules为positive时即成立时，则能得到势函数的值是e的权重次方，否则是e的0次方。